Coeficiente angular ou declividade de uma reta
- Inclinação
Inclinação (θ) de uma reta é o menor ângulo entre a reta e o eixo dos x, orientado no sentido anti-horário, do eixo dos x para a reta (0° ≤ θ < 180°).




- Definição de coeficiente angular
Coeficiente angular ou declividade de uma reta não-vertical é a tangente trigonométrica da sua inclinação, representada por “m”.
m = tg θ
Cálculo do coeficiente angular de uma reta
Sabemos que o valor do coeficiente angular de uma reta é a tangente do seu ângulo de inclinação. Através dessa informação podemos encontrar uma forma prática para obter o valor do coeficiente angular de uma reta sem precisar fazer uso do cálculo da tangente.
Vale ressaltar que se a reta for perpendicular ao eixo das abscissas, o coeficiente angular não existirá, pois não é possível determinar a tangente do ângulo de 90º.
Para representarmos uma reta não vertical em um plano cartesiano é preciso ter no mínimo dois pontos pertencentes a ela. Desse modo, considere uma reta s que passa pelos pontos A(xA, yA) e B(xB, yB) e possui um ângulo de inclinação com o eixo Ox igual a α.
Prolongado a semirreta que passa pelo ponto A e é paralela ao eixo Ox formaremos um triângulo retângulo no ponto C.
O ângulo A do triângulo BCA será igual ao da inclinação da reta, pois, pelo Teorema de Tales, duas retas paralelas cortadas por uma transversal formam ângulos correspondentes iguais.
Levando em consideração o triângulo BCA e que o coeficiente angular é igual à tangente do ângulo de inclinação, teremos:
tgα = yB – yA / xB – xA
Portanto, o cálculo do coeficiente angular de uma reta pode ser feito pela razão da diferença entre dois pontos pertencentes a ela.
m = tgα = Δy / Δx

- Exemplo
Qual é o coeficiente angular da reta que passa pelos pontos A (–1,3) e B (–2,4)?
m = Δy/Δx
m = 4 - 3 / (-2) - (-1)
m = 1 / -1
m = -1
Exercícios
- Dica: Faça-os e depois confira os seus resultados na SOLUÇÃO abaixo.
1) O coeficiente angular da reta que passa pelos pontos A (2,6) e B (4,14) é:
2) O coeficiente angular da reta que passa pelos pontos A (8,1) e B (9,6) é:
Solução
1) O coeficiente angular da reta que passa pelos pontos A (2,6) e B (4,14) é:
m = Δy/Δx
m = 14 – 6/4 – 2
m = 8/2
m = 4
2) O coeficiente angular da reta que passa pelos pontos A (8,1) e B (9,6) é:
m = Δy/Δx
m = 6 – 1/9 – 8
m = 5/1
m = 5
Alinhamento de três pontos
Três pontos não alinhados em um plano cartesiano formam um triângulo de vértices A(xA, yA), B(xB, yB) e C(xC, yC). A sua área poderá ser calculada da seguinte forma:

Para que exista a área do triângulo esse determinante deverá ser diferente de zero. Caso seja igual a zero os três pontos, que eram os vértices do triângulo, só poderão estar alinhados.
Portanto, podemos concluir que três pontos distintos A(xA, yA), B(xB, yB) e C(xC, yC) estarão alinhados se o determinante correspondente a eles for igual a zero.
Exemplo:
Verifique se os pontos A(0,5), B(1,3) e C(2,1) são ou não colineares (são alinhados).
O determinante referente a esses pontos é . Para que sejam colineares, o valor desse determinante deve ser igual à zero.
= 10 + 1 – 6 – 5 = 9 – 6 – 5 = 5 – 5 = 0
Portanto, os pontos A, B e C estão alinhados.
Exercício
1) Determine X, sabendo que X estar contido no conjunto do números reais, os pontos são A(3,5), B(1,3) e C(x,1) sejam vértices de um triângulo.

Ponto médio de um segmento da reta
O segmento de reta possui inúmeros pontos alinhados, mas somente um deles irá dividir o segmento em duas partes iguais. A identificação e a determinação do ponto médio de um segmento de reta será demonstrado com base na ilustração a seguir.
Se o ponto fosse A (2,1) e B (3,4), qual seria as coordenadas do ponto médio?
Utilizando o Teorema de Tales, podemos dizer que:
AM = A1M1
MB M1B1
Os segmentos AM e MB são iguais, pois M é o ponto médio de A e B, assim podemos escrever:
1 = A1M1
M1 B1
x A = 2, então A1M1 = xM – 2
x B = 3, então M1B1 = 3 – xM
Substituindo A1M1 = xM – 2 e M1B1 = 3 – xM em 1 = A1M1, teremos:
M1B1
1 = A1M1
M1B1
1 = xM – 2
3 – xM
xM – 2 = 3 – xM
2xM = 3 + 2
xM = 3+2
2
xM = 5/2
Podemos concluir que a abscissa xM é a media entre as abscissas xA e xB, portando yM será a mediana de yA e yB.
y M = 4 + 1
2
y M = 5/2
Portanto, o ponto médio M terá coordenadas iguais a (5/2, 5/2).
Assim, a forma geral para o cálculo das coordenadas de um ponto médio será:
xM = xA + xB
2
yM = yA + yB
2
Exercício sobre Estatística
1) Um dado foi laçado 50 vezes. A tabela a seguir mostra os seis resultados possíveis e suas respectivas freqüências de ocorrência.
Resultado |
1 |
2 |
3 |
4 |
5 |
6 |
Frequência |
7 |
9 |
8 |
7 |
9 |
10 |
A freqüência do aparecimento de um número ímpar foi de
a) 2/5
b) 11/25
c) 12/25
d) 1/2
e) 13/25
2) O gráfico representa a taxa de desemprego na grande São Paulo, medida nos meses de abril, segundo o Dieese:
Analisando o gráfico, podemos afirmar que a maior variação na taxa de desemprego na Grande São Paulo ocorreu no período de
a) abril de 1985 a abril de 1986
b) abril de 1995 a abril de 1996
c) abril de 1997 a abril de 1998
d) abril de 2001 a abril de 2002
5) O índice de confiabilidade na economia é um número entre 0 e 100 que mede a confiança dos empresários na economia brasileira. Os gráficos ilustram os valores desses índices para grandes e médios empresários, de outubro de 2002 a outubro de 2003, em dados trimestrais.
Analise a veracidade das afirmações seguintes, escrevendo V para verdadeiro e F para falso, acerca dos índices de confiabilidade na economia brasileira dos grandes e médios empresários, representados no gráfico anterior. O crescimento e decrescimento citados nas afirmações são relativos ao trimestre anterior.
( ) O índice dos médios empresários sempre cresceu, de jan. 2003 a out. 2003.
( ) Quando o índice dos médios empresários cresceu, ocorreu o mesmo com o índice do grandes empresários.
( ) Quando o índice dos grandes empresários decresceu, o índice dos médios empresários decresceu.
( ) O índice dos grandes empresários sempre foi superior ao índice dos médios empresários.
( ) Em outubro, o crescimento percentual do índice dos grandes empresários foi igual ao dos médios empresários.
6) Na dose certa
O psiquiatra Içami Tiba diz que amor em excesso não é bom na educação dos filhos. A revista Veja quis saber se os leitores concordam com essa afirmação. O resultado:
Considerando que o diagrama representa os percentuais de respostas de 3700 pessoas, o número de pessoas que discordam do psiquiatra é:
a) 3145
b) 2960
c) 2886
d) 2775
7) Preocupada com a sua locadora, Marla aplicou uma pesquisa com um grupo de 200 clientes escolhidos de forma aleatória, sobre a quantidade de filmes que estes locaram no primeiro semestre de 2011. Os dados coletados estão apresentados na tabela a seguir:
Número de filmes alugados |
|
Número de filmes |
Frequência |
0 |
25 |
1 |
30 |
2 |
55 |
3 |
90 |
Total |
200 |
A média, a moda e a mediana destes dados são, respectivamente, os seguintes:
a) 2,05; 3; 2
b) 1,5; 2; 3
c) 1,5; 3; 3
d) 1,5; 3; 2
e) 2,05; 2; 3
8) As notas de um candidato em suas provas de um concurso foram: 8,4; 9,1; 7,2; 6,8; 8,7 e 7,2.
A nota média, a nota mediana e a nota modal desse aluno, são respectivamente:
a) 7,9; 7,8; 7,2
b) 7,2; 7,8; 7,9
c) 7,8; 7,8; 7,9
d) 7,2; 7,8; 7,9
e) 7,8; 7,9; 7,2
GABARITO
1) C
2) C
3) FVFVF
4) C
5) A
6 ) A
Bem, aprendemos neste ano letivo de 2013 com nosso professor de matemática que praticar através de listas é uma ótima forma para fixar o conteúdo. Portanto, disponibilizamos uma lista com exercícios para que vocês treinem um pouco e também colocaremos o gabarito ao final.
OBS: Responda e depois confira sua resposta no gabarito!
Boa Sorte!
LISTA DE EXERCÍCIOS SOBRE GEOMETRIA ANALÍTICA
1) Os pontos A = (-4, -2) e B = (-2, 2) pertencem respectivamente aos quadrantes:
a) 1º e 2º
b) 2º e 3º
c) 3º e 2º
d) 4º e 2º
e) 3º e 4º
2) O ponto A = (m+3, n-1) pertence ao 3º quadrante, para os possíveis valores de m e n:
a) m > 3 e n < 1
b) m < 3 e n > 1
c) m < -3 e n > 1
d) m < -3 e n < -1
e) m < -3 e n < 1
3) Num triângulo ABC, sendo A = (4,3), B = (0,3) e C um ponto pertencente ao eixo Ox com
AC = BC. O ponto C tem como coordenadas:
a) (2,0)
b) (-2,0)
c) (0,2)
d) (0,-2)
e) (2,-2)
4) O valor de x para que os pontos A = (x, 5), B = (-2,3) e C = (4,1) sejam alinhados é:
a) 8
b) 6
c) -5
d) -8
e) 7
5) Os pontos A = (0,0), B = (3,7) e C = (5, -1) são vértices de um triângulo. O comprimento da
mediana AM é:
a) 3
b) 4
c) 5
d) 6
e) 7
6) O coeficiente angular da reta que passa pelos pontos A = (-1,2) e B = (3,6) é:
a) -1
b) 1/2
c) 3/2
d)3
e) 1
7) A equação da reta que passa pelo ponto (-1,-2) e tem coeficiente angular -1 é:
a) x + y -1 = 0
b) x + y +1 = 0
c) x + y -3 = 0
d) x + y +3 = 0
e) x – y + 3 = 0
8) equação da reta que passa pelos pontos (2, -3) e (8, 1) é:
a) 2x – 3y – 13 = 0
b) -2x – 3y + 13 = 0
c) 3x – 2y + 13 = 0
d) 2x – 3y + 13 = 0
e) 2x + 3y – 13 = 0
9) O ponto de interseção das retas x + 2y = 3 e 2x + 3y – 5 = 0 é:
a) (1,-1)
b) (1,1)
c) (1,2)
d) (-1,1)
e) (2,1)
Resposta da Lista de Exercício sobre Geometria Analítica
1) c
2) e
3) a
4) d
5) c
6) e
7) d
8) a
9) b
Distância entre dois pontos
A base da geometria analítica encontra-se na distância entre dois pontos, pois muitos conceitos são inerentes a esse. Portanto, compreender a expressão algébrica para o cálculo da distância entre dois pontos colabora para uma compreensão fidedigna de outros conceitos da geometria analítica.
A distância permeia todos os conceitos da geometria analítica, pois nesta área da matemática temos a relação de elementos geométricos com os algébricos, e o elemento básico da geometria é o ponto.
Um dos conceitos básicos que vimos na geometria é que a menor distância entre dois pontos é dada por uma reta, contudo, na geometria analítica esses pontos recebem coordenadas no plano cartesiano e por meio dessas coordenadas podemos encontrar o valor da distância entre dois pontos.
Vamos representar dois pontos quaisquer no plano cartesiano.
.png)
Portanto, teremos que a distância entre os pontos A e B será a medida do segmento que tem os dois pontos como extremidade. Por se tratar de dois pontos quaisquer, representaremos as coordenadas desses pontos de maneira genérica.
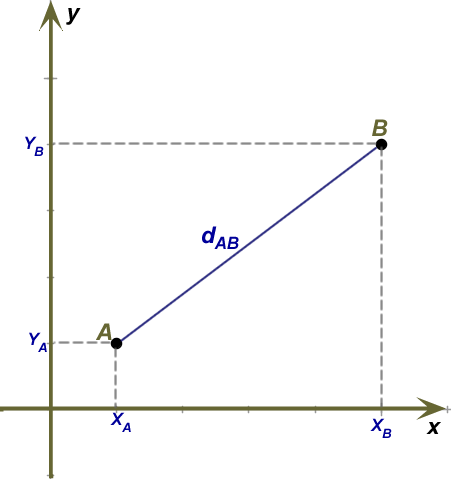
Sabe-se que os eixos coordenados do plano cartesiano são ortogonais, portanto, podemos construir um triângulo retângulo utilizando os pontos A e B, como mostra a figura a seguir.
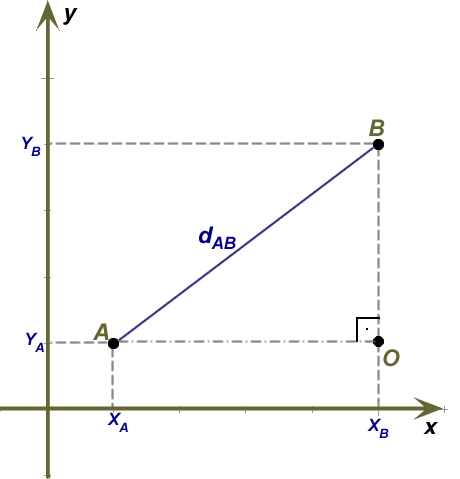
Note que o segmento AB é a hipotenusa do triângulo AOB, e a medida de AB corresponde à distância entre esses dois pontos. Por se tratar de um triângulo retângulo, podemos aplicar o teorema de Pitágoras, no qual teremos:
.png)
Note que basta fazer as diferenças das coordenadas de cada um dos pontos e elevar ao quadrado, contudo são coordenadas do eixo X com coordenadas do eixo X e de forma análoga para as coordenadas do eixo Y.
Calcule a distância entre os pontos: A (4,5) e B(1,1) e represente-os geometricamente.
Como vimos anteriormente, basta aplicar a expressão para o cálculo da distância entre dois pontos. Sendo assim:
.png)
Geometricamente:
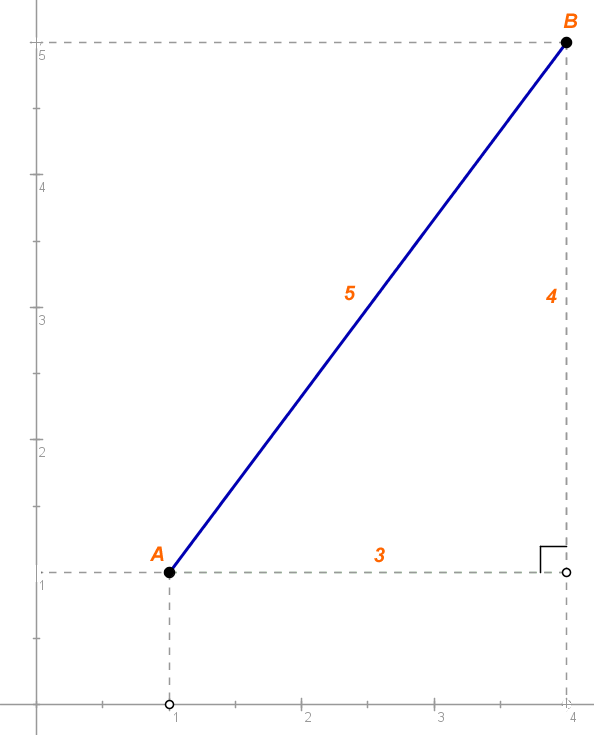
Fonte:https://www.brasilescola.com/matematica/distancia-entre-dois-pontos.htm
Geometria Analítica

A Geometria Analítica, também denominada de coordenadas geométricas, se baseia nos estudos da Geometria através da utilização da Álgebra. Os estudos iniciais estão ligados ao matemático francês René Descartes (1596 -1650), criador do sistema de coordenadas cartesianas.
Os estudos relacionados à Geometria Analítica datam seu início no século XVII, Descartes, ao relacionar a Álgebra com a Geometria, criou princípios matemáticos capazes de analisar por métodos geométricos as propriedades do ponto, da reta e da circunferência, determinando distâncias entre eles, localização e pontos de coordenadas.
Uma característica importante da G.A. se apresenta na definição de formas geométricas de modo numérico, extraindo dados informativos da representação. Com base nesses estudos, a Matemática passa a ser vista como uma disciplina moderna, capaz de explicar e demonstrar situações relacionadas ao espaço. As noções intuitivas de vetores começam a ser exploradas de forma contundente, na busca por resultados numéricos que expressem as ideias da união da Geometria com a Álgebra.
Os vetores constituem a base dos estudos do espaço vetorial, objetos que possuem as características relacionadas a tamanho, direção e sentido. Os vetores são muito utilizados na Física, como ferramenta auxiliar nos cálculos relacionados à Cinemática Vetorial, Dinâmica, Campo Elétrico entre outros conteúdos relacionados.
Os cientistas Isaac Newton e Gottfried Wilhelm Leibniz concentraram estudos na Geometria Analítica, que serviu como base teórica e prática para o surgimento do Cálculo Diferencial e Integral, muito utilizado atualmente na Engenharia.
Podemos relacionar os seguintes tópicos ao estudo da G.A.:
Estudo Analítico do Ponto
Plano Cartesiano
Distância entre dois pontos
Ponto médio de um segmento
Condição de alinhamento de três pontos
Estudo da Reta
Equação geral e reduzida da reta
Intersecção entre retas
Paralelismo
Perpendicularidade
Ângulos entre retas
Distância entre ponto e reta
Estudo da Circunferência
Equação geral e reduzida da circunferência
Posições relativas entre ponto e circunferência
Posições relativas entre reta e circunferência
Problemas relacionados à tangência
Estudo das Cônicas
Elipse
Hipérbole
Parábola Intersecção entre cônicas
Retas tangentes a uma cônica
Fonte: https://www.brasilescola.com/matematica/geometria-analitica.htm
Por Marcos Noé
Graduado em Matemática
Variância e Desvio Padrão
A Variância e o Desvio Padrão são consideradas medidas de dispersão e utilizadas nas situações em que grupos com médias de valores iguais, possuem características diferentes. A Variância estabelece os desvios em relação à média aritmética e o Desvio Padrão analisa a regularidade dos valores. Vamos através de um exemplo prático, demonstrar uma aplicação básica envolvendo as duas medidas.
Na preparação para os jogos Olímpicos de Atenas, três atletas do salto em altura ao realizarem um treinamento diário, consideraram seus quatro melhores saltos em centímetros. Veja:
.jpg)
Dentre os atletas, a melhor média foi a do Atleta Z, veja:
Atleta X = (144 + 171 + 150 + 138) / 4 = 150,75
Atleta Y = (146 + 170 + 152 + 137) / 4 = 151,25
Atleta Z = (145 + 169 + 154 + 140) / 4 = 152
Atleta W = (150 + 167 + 149 + 141) / 4 = 151,75
Em situações que envolvam disputas olímpicas, o atleta com melhor média, às vezes não é considerado o mais indicado, pois verifica-se a questão da regularidade dos resultados obtidos. É referente a esses casos que aplicamos os cálculos ligados à Variância e ao Desvio Padrão.
Lembre-se de que o desvio padrão consiste na raiz quadrada da variância.
Cálculo da Variância e do Desvio Padrão
.jpg)
Atleta X
.jpg)
Atleta Y
.jpg)
Atleta Z
.jpg)
Atleta W
.jpg)
O atleta que obteve o menor Desvio Padrão deve ser considerado o de melhor regularidade em resultados. Dessa forma, temos que o atleta W se enquadra nessa condição de melhor regularidade.
Fonte:https://www.mundoeducacao.com/matematica/variancia-desvio-padrao.htm
Exercícios resolvidos sobre MA
1.Calcule a média das idades de um determinado grupo de pessoas, sabendo que as idades dessas pessoas são: 18, 19, 20, 32, 40, 25, 24, 19,18, 22, 25, 26, 32, 36, 41, 40, 28, 36, 22, 41.
Resposta:
18+19+20+32+40+25+24+19+18+22+25+26+32+36+41+40+28+36+22+41 / 20 = 564/20 = 28,2
2. Dada a tabela de frequências abaixo, determine a média das idades:
IDADE |
FA |
| 18 | 5 |
| 19 | 3 |
| 20 | 4 |
| 21 | 8 |
| 22 | 9 |
| 30 | 6 |
| 36 | 2 |
| 38 | 4 |
| 40 | 5 |
| 41 | 4 |
TOTAL |
50 |
Resposta:
18x5+19x3+x20x4+21x8+22x9+30x6+36x2+38x4+40x5+41x4/50 = 8.609/50 = 172,18
3. Dada a tabela de frequência abaixo, determine a média das alturas:
| ALTURA | FA |
| 1,44 Ⱶ 1,50 | 2 |
| 1,50 Ⱶ 1,56 | 6 |
| 1,56 Ⱶ 1,62 | 4 |
| 1,62 Ⱶ 1,68 | 12 |
| 1,68 Ⱶ 1,74 | 15 |
| 1,74 Ⱶ 1,80 | 8 |
| 1,80 Ⱶ 1,86 | 3 |
TOTAL |
50 |
Resposta:
1,44+1,50 = 2,94/2 = 1,47x2 = 2,88
1,50+1,56 = 3,06/2 = 1,53x6 = 9,18
1,56+1,62 = 3,18/2 = 1,59x4 = 6,36
1,62+1,68 = 3,30/2 = 1,65x12 = 19,8
1,68+1,74 = 3,42/2 = 1,71x15 = 25,65
1,74+1,80 = 3,54/2 = 1,77x8 = 14,16
1,80+1,86 = 3,66/2 = 1,83x3 = 5,49
2,88+9,18+6,36+19,8+25,65+14,16+5,49 = 95,58
MA = 95,58/50 = 1,9116
Medidas de tendência central
Média Aritmética (MA)
A média aritmética é considerada uma medida de tendência central e é muito utilizada no cotidiano. Surge do resultado da divisão do somatório dos números dados pela quantidade de números somados.
Mediana
Mediana é uma medida de tendência central que indica exatamente o valor central de uma amostra de dados.
Moda
Moda é a medida de tendência central que consiste no valor observado com mais frequência em um conjunto de dados.
Tipos de Gráficos
Os gráficos constituem uma forma clara e objetiva de apresentar dados estatísticos. A intenção é a de proporcionar aos leitores em geral a compreensão e a veracidade dos fatos. De acordo com a característica da informação precisamos escolher o gráfico correto. Os mais usuais são: gráfico de segmentos, gráfico de barras e gráfico de setores.
Gráfico de Segmento ou gráfico de linhas
Objetivos: simplicidade, clareza e veracidade.
.jpg)
Gráfico de Barras horizontal e vertical
Objetivo: representar os dados através de retângulos, com o intuito de analisar as projeções no período determinado.
.jpg)
Gráfico de setores
Objetivos: expressar as informações em uma circunferência fracionada. É um gráfico muito usado na demonstração de dados percentuais.
.jpg)
Fonte:https://www.mundoeducacao.com/matematica/tipos-graficos-1.htm
Elementos Fundamentais
Fala galera! Andamos sumidas, mas voltamos com força total!
Bom, como o título sugere, irá contar noções da estatística importantes no momento da interpretação dos gráficos. E os elementos são:
População: conjunto de elementos. Podendo ser pessoas, objetos etc.
Amostra: parte da população.
Variável: bom, isso vai depender do fundamento da pesquisa. Ex: Marcas de celulares mais vendidos em ''X'' loja. Resposta: Samsung, Apple, Nokia etc.
Na variável encontramos:
Variável qualitativa: nesta os elementos pesquisados possuem qualidades. Além disso, dizemos que esta variável pode ser ordinal, se houver a presença da ordem, ou nominal, quando não há a presença da ordem.
Variável quantitativa: os elementos pesquisados são numéricos. Esta pode ser discreta, quando os números são inteiros, ou contínua, quando são medidas.
Ex: Discreta: números de computadores em uma lan house.
Contínua: altura (1,78 m)
Frequência Absoluta [FA]: valor exato; números de vezes que o valor da variável é citado.
Frequência Relativa [FR]: valor representado através da porcentagem.
Vale deixar claro que nos baseamos no nosso livro didático (Matemática Contexto & Aplicações - Dante volume3).
Fiquem ligado, novas publicações viram!
Você sabe o que é Estatística?
É a área da Matemática que coleta, analisa e interpreta dados numéricos para o estudo de fenômenos naturais, econômicos e sociais. O estatístico planeja e coordena o levantamento de informações por meio de questionários, entrevistas e medições. Organiza, analisa e interpreta os resultados para explicar fenômenos sociais, econômicos ou naturais. Cabe a ele montar banco de dados para os mais diversos usos. Na indústria, acompanha os testes de qualidade, ajuda a fazer previsão de vendas e desenvolve modelos matemáticos para ajustá-los a situações práticas.
https://guiadoestudante.abril.com.br/profissoes/ciencias-exatas-informatica/estatistica-686049.shtml
Notícias
Site lançado
06/09/2013 00:01Bem-vindo ao nosso site
Seja bem-vindo, ainda estamos em aperfeiçoamento e desculpa os transtornos ;)
Oi, gente! Chegamos com a corda toda com várias atualizações.
Mas hoje vim fazer uma correção do vídeo Distância entre dois pontos. No segundo exemplo, quando falo 4² está incorreto. O certo é (-4²).
A outra observação é a seguinte: após achar a raiz do número deve-se colocar u.c que siginifica unidade de medida.
Tudo jóia? Qualquer dúvida, estamos à disposição.



